학교에서 매달 백준 등에 있는 어려운 문제를 하나씩 해결하는 과제가 나왔습니다. 따라서 오늘부터는 백준에 있는 여러 문제를 풀어보려고 합니다.
https://www.acmicpc.net/problem/17951
17951번: 흩날리는 시험지 속에서 내 평점이 느껴진거야
시험지를 12, 7, 19, 20과 17, 14, 9, 10 으로 나누면 맞은 문제 개수의 합의 최소는 50이다.
www.acmicpc.net
사전 탐구
3월 과제의 주제는 탐색기반설계 및 관계기반설계 탐구입니다. 그럼 먼저 탐색기반설계와 관계기반설계가 무엇인지를 알아봐야겠죠.
먼저, 탐색기반설계에 대해 알아보겠습니다. 탐색기반설계란 탐색기반 알고리즘을 설계하는 것입니다. 여기서 탐색기반 알고리즘이란 컴퓨팅 시스템의 탐색 능력을 기반으로 문제 해결을 위한 해를 찾는 알고리즘을 뜻합니다.
탐색기반설계 방법은 다음과 같습니다. 먼저, 해가 존재할 수 있는 집합(탐색 공간)을 설정합니다. 이때 탐색 공간은 파일, 폴더, 혹은 특정 범위의 숫자, 문자열 등 다양한 종류가 될 수 있습니다. 이후, 탐색 공간의 크기를 줄여 효율적으로 탐색할 수 있게 하는 것이 탐색기반설계입니다.
탐색 알고리즘은 크게 선형 구조와 비선형 구조로 나뉘며, 선형 구조에는 순차 탐색, 이진 탐색 등이 있고, 비선형 탐색에는 깊이 우선 탐색(DFS), 너비 우선 탐색(BFS) 등이 있습니다.
다음으로 관계기반설계입니다. 관계기반설계란 관계기반 알고리즘을 설계하는 것입니다. 관계기반 알고리즘이란 해를 구하는 행위를 하나의 함수로 표현하고, 이 함수들의 관계를 이용하여 해를 구하는 것입니다.
관계기반설계를 하기 위해서는 먼저 문제의 정의와 상태를 함수로 정의하고, 이 함수들 간의 관계를 점화식 혹은 유사한 형태로 표현해야 합니다. 수학적 귀납법, 점화식 등의 표현을 기반으로 한다고 보시면 됩니다.
관계기반설계에는 분할 정복, 정렬 알고리즘, 다이나믹 프로그래밍(DP) 등이 있습니다. 관계기반설계의 가장 대표적인 예가 재귀함수인데, 재귀함수는 f(n)과 f(n-1) 등 함수들 간의 관계를 이용해서 문제를 해결하는 방법으로 큰 문제를 작은 문제들로 나눠 푸는 분할 정복의 일종입니다.
문제 선정 과정
저는 이 중 저에게 좀 더 친숙하고 자주 들어본 탐색기반설계를 고르기로 했고, 탐색기반설계의 여러 종류 중 이분 탐색(Binary Search)을 선택했는데, 이전에 코드업을 풀거나 할 때 가장 자주 마주친 알고리즘이기도 하고, 학교 수업 때 비슷한 알고리즘을 살짝 배운 기억이 있기 때문입니다. 이렇게 자주 보게 되는 알고리즘이다보니 이번 기회에 공부해두면 나중에 많은 도움이 될 거라고 생각해 이분 탐색을 선택하게 되었습니다.
이후 이분 탐색 문제를 살펴보던 중 누가 봐도 풀고 싶게 생긴 제목을 발견했고, 설정돼있는 문제 상황 등도 맘에 들어서 이 17951번 문제를 풀어보기로 하였습니다.
문제 풀이 전략
문제를 어떻게 풀지 생각하기 전에 어떤 문제인지부터 확인해보도록 하겠습니다.
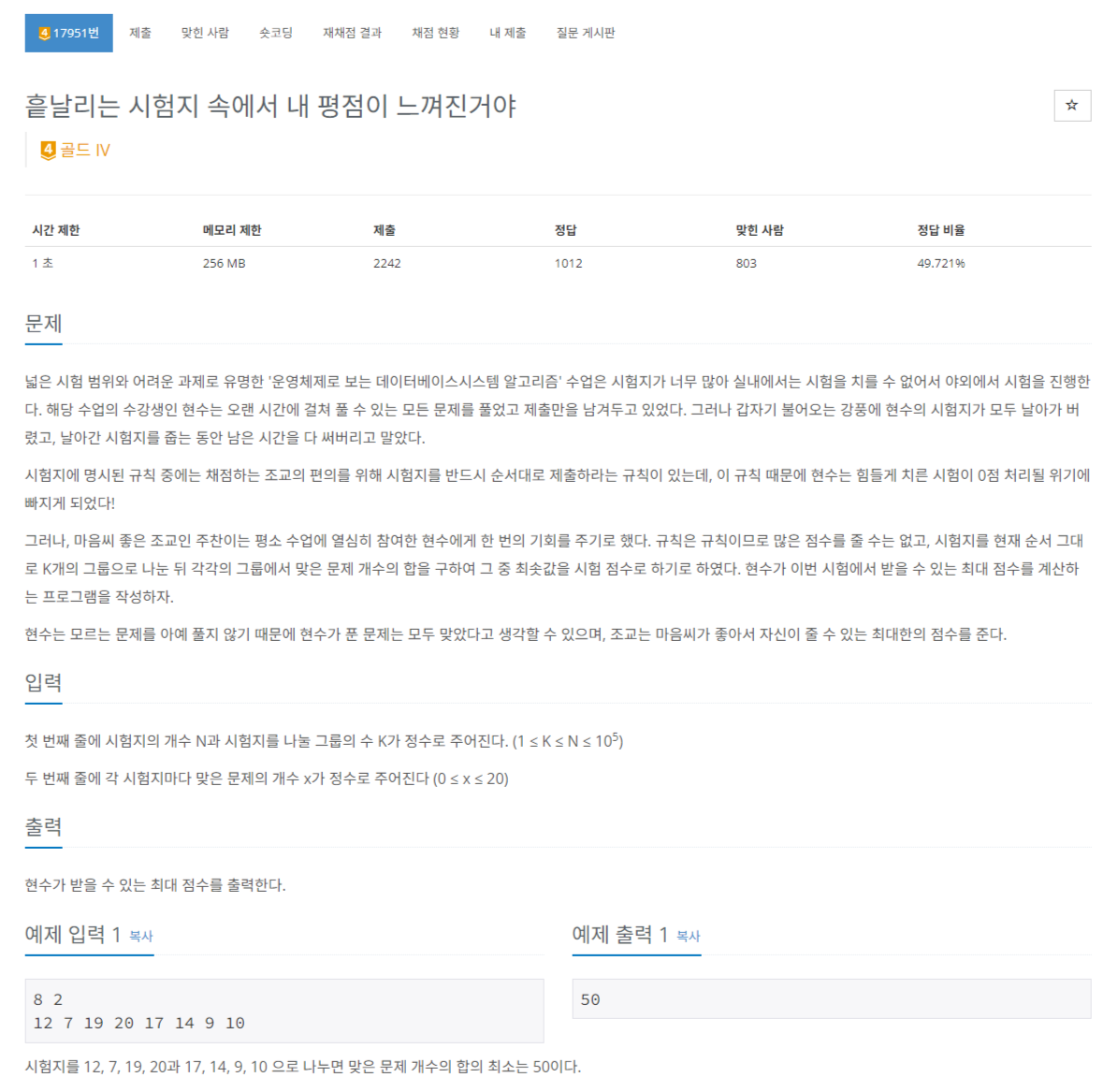
적당히 요약해보자면 N개의 시험지가 있는데 이걸 K개의 그룹으로 나눠 각각의 그룹에서 맞은 시험 문제 수 중 최솟값을 찾는데 그 최솟값이 최대가 되게 하는 문제인 것 같습니다. (말장난...?)
이제 이 문제를 어떻게 풀지 생각해보록 하겠습니다.
먼저, 이분탐색을 진행할 범위를 정하고, 찾고자 하는 최솟값의 최댓값(pivot)을 설정합니다. (적당히 최솟값(left)과 최댓값(right)의 평균)
이제 총 시험점수가 pivot을 넘지 않게 시험지들을 여러 개의 그룹으로 쪼개줘야 합니다. 이는 그리디 알고리즘(Greedy Algorithm)을 사용해 간단하게 해결할 수 있을 것으로 보입니다.
시험점수가 pivot을 넘지 않게 나눴다면 이 때의 그룹 수와 k를 비교해주어야 합니다. 만약 그룹 수가 k보다 작다면 그룹 수를 늘려야 한다는 것이므로 pivot이 줄어들어야 합니다. 그룹 수가 k보다 크다면 그룹 수를 줄여야 하므로 pivot이 커져야 합니다.
알고리즘 설명
1. 이분 탐색 (Binary Search)
이진 탐색이란 데이터가 정렬돼 있는 배열에서 특정한 값을 찾아내는 알고리즘입니다.
이분 탐색은 일반적으로 아래와 같은 과정으로 이루어집니다.
- 배열의 중간에 있는 임의의 요소의 인덱스를 pivot으로 정한다.
- a[pivot]의 값이 찾고자 하는 요소 X와 같다면 탐색 종료
- a[pivot] > X라면 pivot 왼쪽 값에서 다시 탐색
- a[pivot] < X라면 pivot 오른쪽 값에서 다시 탐색
(이를 계속 반복하여 X를 찾아냄)
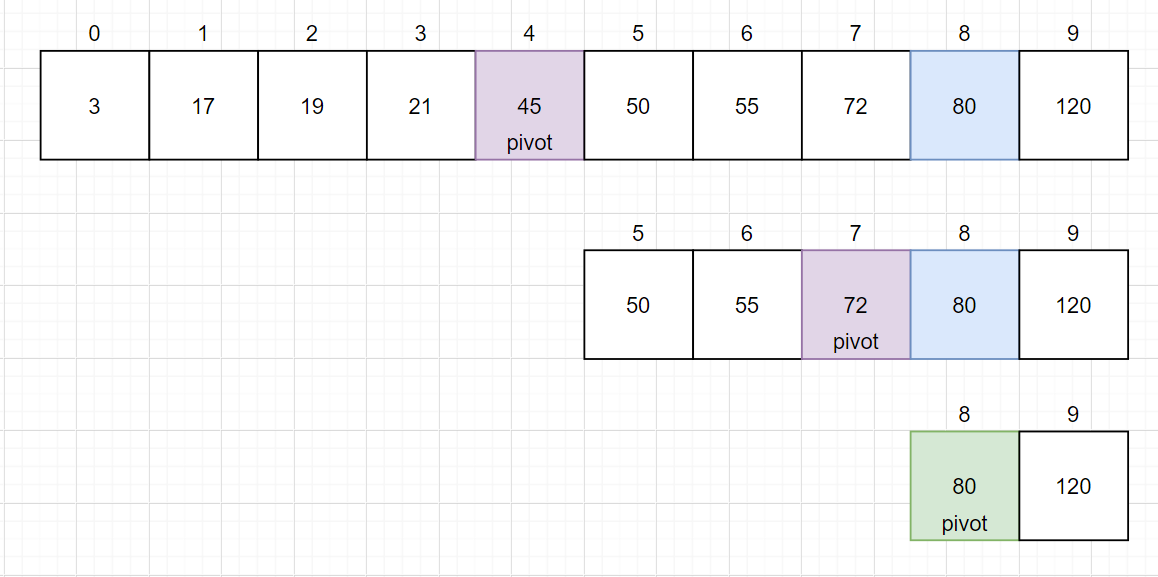
위 사진은 데이터들이 오름차순으로 정렬돼있는 배열에서 80이라는 숫자를 찾아내는 모습을 나타낸 것입니다. 배열의 중간값인 45를 처음 중간값(pivot)으로 정한 뒤, 찾고자 하는 값(80)이 pivot보다 크므로 원래 pivot의 오른쪽 값들을 대상으로 다시 탐색하고, 계속 탐색하여 80을 찾아내는 것을 볼 수 있습니다.
이렇게 이분 탐색은 탐색할 범위를 절반씩 줄여나가므로 O(log n)의 매우 훌륭한 시간복잡도를 갖는다는 장점이 있습니다.
보통은 이런 식으로 데이터들이 정렬돼있는 배열에서 뭔가를 찾을 때 이분 탐색을 사용하지만, 현재 저희의 상황에선 데이터를 정렬할 수 없으므로 단순히 탐색 범위를 반으로 줄이는 데에 사용할 것입니다.
2. 그리디 알고리즘 (Greedy Algorithm)
그리디 알고리즘은 현재 상황에서 가장 좋은 선택을 하는 알고리즘을 말합니다. 다른 그 어떤 것도 고려하지 않고 '현재 상황'에서 가장 좋은 선택만을 고려하기 때문에 그리디 알고리즘으로 꼭 정답을 구해낼 수 있는 건 아닙니다.
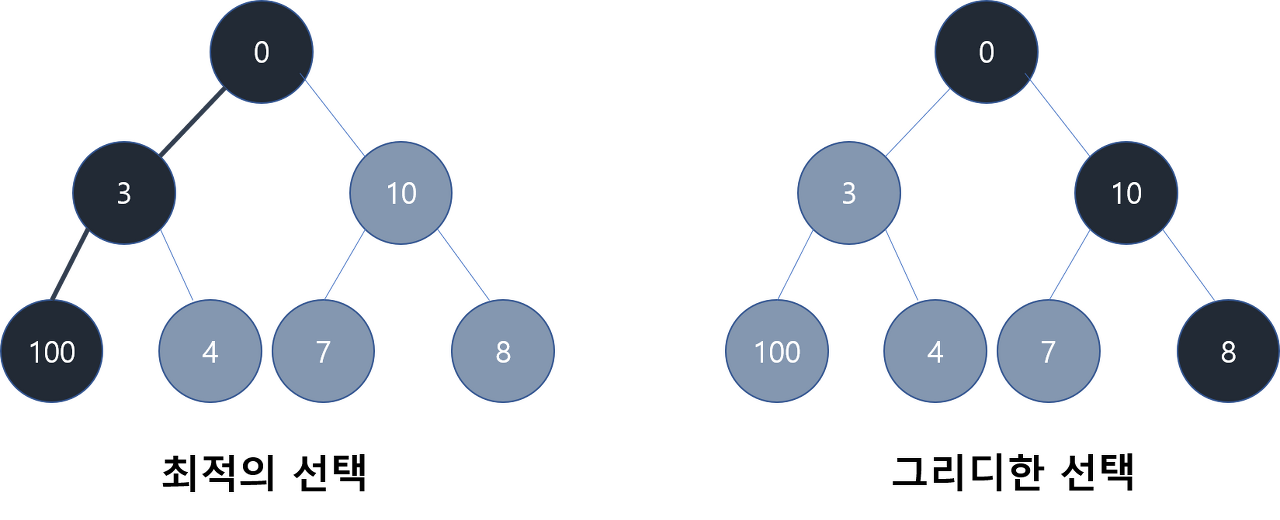
이 사진에서 우리는 노드들의 합의 최댓값이 0-3-100의 순이란 걸 바로 알아챌 수 있습니다. 그러나, 그리디 알고리즘을 사용하면 3과 10이라는 상황만을 보고 판단하기 때문에 이 때 더 좋은 선택인 10을 고르고, 그 이후 7과 8 중에 8을 골라 18이 최댓값이라고 하게 됩니다.
따라서 이러한 문제를 방지하기 위해 그리디 알고리즘을 쓸 때는 '탐욕스러운 선택이 항상 안전하다.', '문제에 대한 최종 해결 방법이 부분 문제에 대해서도 최적의 해결 방법이다.'라는 조건이 만족되어야 합니다.
문제 풀이 과정
이제 문제 풀이 전략도 세우고, 문제를 푸는데 필요한 알고리즘에 대해서도 공부했으니 문제를 풀기 위해 코드를 짜보겠습니다.
먼저, N, K, 그리고 시험지 별 점수들을 입력받는 코드를 짜줍니다.
n, k = map(int, input().split())
score = list(map(int, input().split()))(이 정도는 코드업 기초 100제에서도 쓰인다.)
이후 이분 탐색을 진행할 범위를 지정해주겠습니다.
최솟값과 최댓값을 지정해주어야 하는데, 초기 상태에는 당연히 가능한 가장 적은 점수와 가장 큰 점수를 지정해야겠죠.
left = 0 # 최솟값
right = sum(score) # 최댓값
이제 본격적으로 이분 탐색을 진행해보겠습니다.
이분 탐색은 주로 pivot을 기준으로 탐색을 진행한 뒤, left를 pivot 오른쪽으로 옮기거나, right를 pivot 왼쪽으로 옮기는 식으로 진행됩니다. 따라서 찾고자 하는 값을 찾는 경우는 탐색 범위가 딱 하나로 지정됐을 때, 즉 left와 right가 같을 때라고 할 수 있습니다.
그러므로 이분 탐색을 진행하는 조건은 left <= right라는 것을 쉽게 생각해낼 수 있겠죠.
그리고 탐색을 위해 pivot을 지정할 겁니다. pivot은 주로 배열의 중간값을 사용하는데, 저희는 배열을 사용하는 게 아닌 그냥 pivot을 어떤 기준으로 정해놓고 그 기준과 비교해 범위를 줄이는 것이므로 간단하게 최솟값과 최댓값의 평균으로 지정해도 됩니다. 지금 지정한 pivot이 저희가 구하고자 하는 값이라고 가정하고 연산을 진행한 뒤, 만약 구하고자 하는 값이 아니라면 pivot을 조정하는 식으로 코드를 구성하면 됩니다.
pivot = (left+right)//2 # 중간값
이제 기준값인 pivot까지 정했으니 시험지들을 그룹으로 묶어보겠습니다. 시험지를 묶을 땐 각 그룹의 총 점수가 pivot보다 작아야 합니다. 따라서 그리디 알고리즘을 이용해 score[i]의 값의 누적이 pivot보다 작을때까지 더하고, 커지면 그룹 수를 1 증가시키는 방식으로 코드를 짜면 됩니다.
currentSum = 0 # 현재 그룹의 점수 합
groupCount = 1 # 현재 그룹 수 (최소 한 그룹 존재)
for i in range(n) :
currentSum += score[i]
if currentSum > pivot :
i -= 1
currentSum = 0
groupCount += 1그룹 점수(currentSum)에 시험지 각각의 점수를 더하다가 누적 점수가 pivot보다 커지면 방금 더한 시험지부터 다시 시작해야하므로 i에 1을 빼서 시험지를 이전으로 되돌리게 하였습니다. 그리고 그룹 점수를 0으로 초기화 한 뒤 그룹 수(groupCount)를 1 증가시켰습니다.
이렇게 그룹별로 분류까지 끝냈으므로 이제 구한 그룹 수가 k개인지 확인하고 아닐 경우에 적절한 연산을 해주는 일만 남았습니다. 아까 문제 풀이 전략에서 말했듯 나눈 그룹 수가 k보다 클 때는 pivot을 증가시켜야 합니다. 따라서 이때는 left를 pivot+1로 초기화하고, k 이하이면 right를 pivot-1로 초기화해주면 됩니다.
if groupCount <= k : # 그룹 수 = k 이하 -> 그룹 수 늘려야 함 -> pivot 작아져야함
right = pivot - 1
else :
left = pivot + 1
그리고 while문이 끝났을 때 (right가 left보다 작아졌을 때) left 값(찾고자 하는 값)을 출력하게 해주면 문제 해결입니다!
아래는 전체 코드입니다.
n, k = map(int, input().split())
score = list(map(int, input().split()))
left = 0 # 최솟값
right = sum(score) # 최댓값
while left <= right :
pivot = (left+right)//2 # 중간값
currentSum = 0 # 현재 그룹의 점수 합
groupCount = 1 # 현재 그룹 수 (최소 한 그룹 존재)
for i in range(n) :
currentSum += score[i]
if currentSum > pivot :
i -= 1
currentSum = 0
groupCount += 1
if groupCount <= k : # 그룹 수 = k 이하 -> 그룹 수 늘려야 함 -> pivot 작아져야함
right = pivot - 1
else :
left = pivot + 1
print(left)시행착오
처음에 while문의 반복 조건이 왜 left<=right인지를 이해하지 못했습니다. 그러나 코드의 실행 순서를 천천히 생각해보니 groupCount와 k를 비교하며 만약 우리가 찾고자 하는 값이 결정된다면 pivot = left일 것이고, groupCount와 k가 같을 것이므로 right가 pivot-1이 되어 left보다 작아진다는 것을 이해할 수 있었고, 코드를 성공적으로 작성할 수 있었습니다.
또, 처음 코드를 짤 때 groupCount의 초기값을 0으로 놓고 코드를 짰더니 에러가 났습니다. 근데 결국 마지막에 그룹을 나누면 해당 과정에선 그룹이 2개 생기는 것이나 마찬가지이므로 초기 그룹 수를 1로 지정함으로써 이를 해결할 수 있었습니다.
느낀 점
이번 문제를 풀어보며 이분 탐색에 대해 처음으로 제대로 공부하게 되었고, 슬쩍슬쩍 듣고 볼 때는 굉장히 어려워보이는 알고리즘이었는데, 막상 실제로 코드를 짜며 사용해보니 간단한 알고리즘이었다는 것을 알 수 있었습니다. 이렇게 스스로 공부하여 문제를 해결하니 뿌듯함이 몰려왔고, 앞으로도 이분 탐색 문제를 해결함에 있어 자신감이 생길 것 같다는 생각이 들었습니다.
'프로그래밍 > 문제 풀이' 카테고리의 다른 글
| 나만의 문제 만들기 - [AP 프로그래밍 - 7월 과제] (2) | 2024.07.01 |
|---|---|
| 백준(BaekJoon) 16434번 풀이 - [AP 프로그래밍 - 6월 과제] (0) | 2024.06.01 |
| 백준(BaekJoon) 1167번 풀이 - [AP 프로그래밍 - 5월 과제] (1) | 2024.05.01 |
| 백준(BaekJoon) 1918번 풀이 - [AP 프로그래밍 - 4월 과제] (5) | 2024.04.01 |



