(4월 과제)
2024.04.01 - [프로그래밍/문제 풀이] - 백준(BaekJoon) 1918번 풀이 - [AP 프로그래밍 - 4월 과제]
5월 과제는 자료구조입니다. 자료구조 문제 중 백준 1167번을 풀어보도록 하겠습니다.
https://www.acmicpc.net/problem/1167
1167번: 트리의 지름
트리가 입력으로 주어진다. 먼저 첫 번째 줄에서는 트리의 정점의 개수 V가 주어지고 (2 ≤ V ≤ 100,000)둘째 줄부터 V개의 줄에 걸쳐 간선의 정보가 다음과 같이 주어진다. 정점 번호는 1부터 V까지
www.acmicpc.net
사전 탐구
5월의 주제는 4월 주제와 같이 자료구조입니다. 따라서 자료구조에 대해 알아봐야하지만..? 이미 4월달에 다 정리해서 올렸으므로 그걸로 대체(날먹)하겠습니다.
2024.03.24 - [프로그래밍/문제 풀이] - 백준(BaekJoon) 1918번 풀이 - [AP 프로그래밍 - 4월 과제]
백준(BaekJoon) 1918번 풀이 - [AP 프로그래밍 - 4월 과제]
(3월 과제) 2024.03.23 - [프로그래밍/문제 풀이] - 백준(BaekJoon) 17951번 풀이 - [AP 프로그래밍 - 3월 과제] 백준(BaekJoon) 17951번 풀이 - [AP 프로그래밍 - 3월 과제] 학교에서 매달 백준 등에 있는 어려운 문
olzl07.tistory.com
문제 선정 과정
4월달에는 선형 자료구조의 예시인 스택에 관한 문제를 풀어봤으니 이번에는 비선형 자료구조 중 하나에 관한 문제를 풀어보고자 하였습니다. 특히 비선형 자료구조 중 '트리'는 진짜 유명하고 트리를 이용해 푸는 문제가 정말 많아 제가 많은 문제를 풀지 못한 아픈 기억이 있습니다.
따라서 이번에 과제를 하며 공부를 해보고자 5월의 자료구조는 트리로 골랐고, '트리의 지름'이라는 굉장히 트리트리한(?) 문제가 있어 이 문제를 선택하게 되었습니다.
문제 풀이 전략
이번에도 역시 어떤 문제인지를 먼저 알아보겠습니다.

문제를 간략히 요약해보자면 여러 노드들이 연결되어있는 트리가 주어지고, 노드들 사이의 거리가 주어집니다. 이때, 트리에서 임의의 두 노드 사이의 거리가 최대가 되는 값을 구하면 되는 간단해보이는 문제입니다.
이제 문제를 어떻게 풀지를 생각해보도록 하겠습니다.
이 문제를 풀기 위해서는 알아야하는 가장 중요한 성질이 한 가지 있습니다. 바로 어떤 임의의 한 노드에서 거리가 가장 먼 노드는 이 트리의 지름 중 한 점이라는 것입니다. 예를 들어보겠습니다.

이 트리에서 지름(최대 거리)은 15-11-9-10으로 9번 노드와 12번 노드가 지름의 두 노드입니다. 그렇다면 임의의 점 (10번 노드)에서 가장 거리가 먼 노드는 어디일까요? 최대 거리는 4-11-9-10으로 10번 노드와 가장 거리가 먼 노드는 12번 노드임을 알 수 있습니다. 다른 점 (8번 노드)에서 최대 거리 역시 7-5-3-2-11-15로 가장 먼 노드는 9번 노드, 즉 트리의 지름 중 한 노드임을 알 수 있습니다. 저는 이러한 성질을 이용하여 이 문제를 해결해볼 것입니다.
따라서 이 문제를 해결하는 과정은 다음과 같습니다. 먼저, 임의의 한 노드를 골라 그 노드에서 가장 거리가 먼 노드를 찾습니다. 그렇다면 거기는 지름 중 하나의 노드이겠죠. 그리고 방금 찾은 노드에서 다시 거리가 가장 먼 노드를 찾으면 그 두 노드가 지름이 되는 것입니다.
방법은 간단하지만, 제한시간 내에 거리가 가장 먼 노드를 찾는 것이 관건일 것 같습니다. 따라서 저는 DFS(깊이 우선 탐색)을 이용해 효율적으로 거리가 최대인 노드를 찾게 할 것입니다.
자료 구조 / 알고리즘 설명
1. 트리 (Tree)
- 트리란?
트리란 노드들이 나무 가지처럼 연결된 비선형 자료구조입니다. 또, 트리 내에 하위 트리가 있고, 그 하위 트리 내에 다른 하위 트리가 있는 재귀적 자료구조이기도 합니다.

트리는 자료 구조 중 '그래프(Graph)'의 일종이기도 합니다.
- 트리 용어


| 용어 | 의미 | 예시 (위 사진) |
| 노드(정점) (Node) | 트리를 구성하는 기본 요소 | A, B, C ... J |
| 간선 (Edge) | 노드 사이의 연결선 | |
| 루트 노드 (Root Node) | 부모가 없는 최상위 노드 | A |
| 리프 노드 (Leaf Node) | 자식이 없는 최하위 노드 | H, I, J, F, G |
| 부모 노드 (Parent Node) | 자식 노드를 가진 노드 | A, B, C ... |
| 자식 노드 (Child Node) | 부모 노드의 하위 노드 | B, C, D ... |
| 형제 노드 (Sibiling Node) | 같은 부모를 갖는 노드 | H & I, D & E, F & G ... |
| 깊이 (Depth) | 루트 노드에서 어떤 노드까지의 간선 수 | B = 1, H = 3, F = 2 ... |
| 너비 (Breadth) | 리프 노드의 수 | 5 |
| 거리 (Distance) | 두 노드 사이 최단 경로의 간선 수 | D & J = 2, H & G = 4 ... |
| 차수 (Degree) | 어떤 노드의 자식 노드의 수 | D = 2, E = 1 ... |
- 트리의 특징
- 하나의 루트 노드 & 0개 이상의 하위 트리로 이루어짐
- 비선형, 재귀적 자료구조
- 순환(Loop)을 갖지 않고 연결된 무방향 그래프 구조
- 노드 간에 부모-자식 관계를 갖는 계층형 자료구조
- 노드가 n개이면 간선의 수 = 항상 n-1개
- 트리의 종류
1) 편향 트리 (Skew Tree) : 모든 노드가 자식을 하나만 갖는 트리
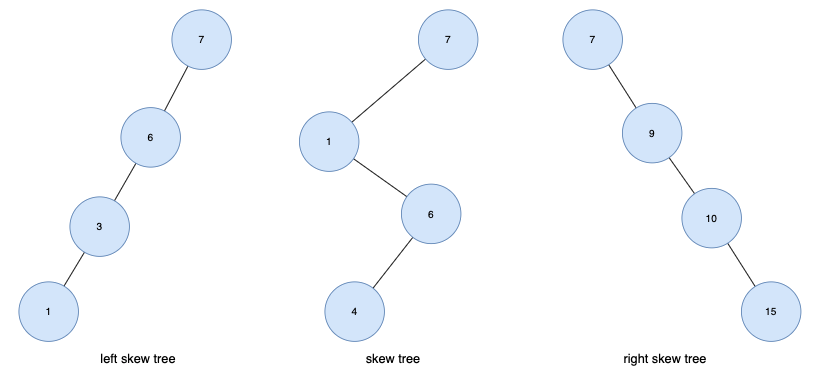
2) 이진 트리 (Binary Tree) : 모든 노드의 차수 = 2 이하인 트리
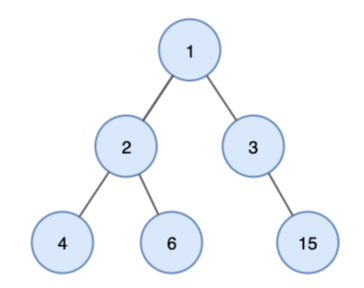
2. 깊이 우선 탐색 (DFS (Depth First Search))
- DFS란?
DFS는 임의의 노드에서 시작해 다음 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방법으로, 비선형 탐색 알고리즘의 일종입니다.
ex) 미로를 탐색할 때 한 방향으로 갈 수 있을 때까지 가다 더 이상 갈 수 없게 되면 가장 가까운 갈림길로 돌아와서 이곳으로부터 다른 방향으로 다시 탐색을 진행하는 방법등이 있습니다.
- DFS의 진행 과정
DFS는 부모 노드에서 한 자식 노드를 고르고 그 자식 노드에서 또 자식 노드를 고르고... 하는 과정을 반복하여 하나의 자식 노드 안에 있는 모든 노드를 탐색하고 다음 자식 노드로 넘어가는 방식으로 진행됩니다.
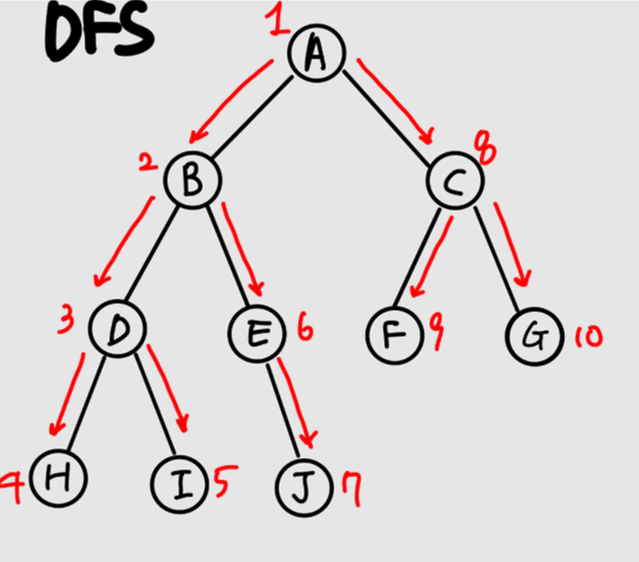
위 사진에서 볼 수 있듯이 A에서 시작해 B로 간 후에 C가 아닌 D로 가는, 즉 B라는 하위트리 내의 모든 노드를 탐색하는 과정으로 진행됩니다.
- DFS의 특징
- 자기 자신을 호출하는 순환 알고리즘의 형태를 띔
- 무한 루프를 방지하기 위해 반드시 어떤 노드에 방문했는지를 체크
DFS는 총 2가지의 방법으로 구현할 수 있습니다.
1. 재귀함수 이용 : 방문하지 않은 자식 노드가 없을 때까지 노드를 탐색하는 함수 (자기 자신)를 반복 호출
2. 스택 이용 : 방문했던 노드들을 스택에 저장했다가 후에 꺼내어 작업
이번에 저는 저 두 가지의 방법 중 재귀함수를 이용해 DFS를 구현할 것입니다. 재귀함수를 이용한 DFS 구현은 주로 다음과 같이 진행됩니다. '어떤 노드에 방문 → 이 노드는 방문했다고 표시 → 이 노드의 자식 노드를 방문하지 않았다면 해당 자식 노드에 대해 또 탐색 & 방문했다면 이전 함수로 계속 돌아감 → 아직 방문하지 않은 새로운 노드가 나올때까지 위로 올라감'
따라서 이후 코드에서도 이런 방식으로 DFS를 구현해보겠습니다.
- DFS의 시간복잡도
DFS는 인접리스트와 인접행렬로 표현하여 탐색할 수 있습니다. 이때, 인접 리스트로 그래프를 표현하면 O(N+E) (N : 노드 수, E : 간선 수), 인접 행렬로 그래프를 표현하면 O(N^2) (N : 노드 수)의 시간복잡도를 가집니다.
문제 풀이 과정
이제 드디어 문제를 풀어보도록 하겠습니다.
먼저, 파이썬 내의 재귀호출제한을 풀어야합니다. 노드 수가 최대 10만이기 때문에 시간초과가 날 수 있기 때문입니다. 저는 제한을 적당히 10^9 정도로 하였습니다.
import sys
sys.setrecursionlimit(10**9)
이후 n을 입력받고 노드들 간의 연결을 저장할 (n+1)개의 하위 리스트가 있는 이중리스트를 생성해줍니다. n개가 아니라 n+1개인 이유는 노드 번호가 0이 아닌 1부터 시작하기 때문입니다. 또 특정 노드에 방문했는지를 확인하기 위한 리스트 (역시 n+1개)와 특정 노드까지의 거리와 노드 번호를 저장할 리스트도 생성해줍니다.
n = int(input())
graph = [[] for _ in range(n+1)] # 그래프 제작
visited = [0] * (n+1) # 방문했는지 확인
length = [] # 어떤 노드 ~ 다른 노드까지의 길이
이제 입력을 받아줍니다. 먼저, 줄 마지막엔 -1이 반드시 입력되므로 한 줄을 입력받고 -1이 나오기 전까지 (연결된 노드 번호, 거리)를 튜플의 형태로 graph 리스트에 저장해줍니다. 이 과정을 n번 반복하면 됩니다.
for i in range(n) :
temp_input = list(map(int, input().split())) # 우선 한 줄 입력받기
j = 1
while temp_input[j] != -1 :
graph[temp_input[0]].append((temp_input[j], temp_input[j+1])) # -1이 입력되기 전까지 연결된 노드, 거리를 저장
j += 2
이후 최대 거리를 찾는 함수를 정의해줘야 합니다. (DFS!) 함수의 매개변수는 노드 번호와 누적 거리로 지정해주었습니다. 먼저, 이 노드에 방문했다는 표시를 남기기 위해 visited[node]를 1로 지정해주었습니다. 그리고 현재 노드의 요소들(연결돼있는 자식 노드, 거리)에 접근하였고, 만약 현재 노드에 방문하지 않은 자식 노드가 있다면 해당 자식 노드에 대해 다시 한 번 함수를 실행하게 하였습니다. 또, 모든 자식 노드에 방문했다면 현재까지의 거리와 마지막 자식 노드의 번호를 length 리스트에 저장하게 하였습니다.
def DFS(node, temp) :
visited[node] = 1 # 일단 이 노드는 방문 처리
for child_node, distance in graph[node] :
if visited[child_node] == 0 : # 자식 노드에 방문 안 했다면
DFS(child_node, temp + distance)
length.append([temp, node]) # 방문 안 한 자식 노드가 없다면 -> 리프 노드라면 길이 저장
이제 단순한 작업만 남았습니다. 먼저, 아무 노드나 골라서 DFS 함수를 실행해 가장 거리가 먼 노드 (지름 중 하나)를 찾고, 각종 배열을 초기화한 뒤, 그 노드에 대해 한 번 더 DFS 함수를 실행한 뒤 거리의 최댓값을 찾으면 문제 해결입니다!
DFS(1, 0) # 그냥 1번 노드에서 시작
temp_maxLength = max(length, key = lambda x: x[0]) # lengt의 특정 열에서만 최댓값 찾는 함수
diameter_point1 = temp_maxLength[1] # 지름 중 한 점
visited = [0] * (n+1)
length = [] # 배열들 초기화
DFS(diameter_point1, 0)
maxLength = max(length, key=lambda x: x[0])
print(maxLength[0]) # 최대 길이 출력여기 쓰인 lambda 구문은 그냥 length가 (거리, 노드 번호)들이 집합돼있는 리스트의 형태라 '거리'에 관해서만 최댓값을 찾게 해준다고 생각하시면 됩니다.
다음은 전체 코드입니다.
import sys
sys.setrecursionlimit(10**9)
n = int(input())
graph = [[] for _ in range(n+1)] # 그래프 제작
visited = [0] * (n+1) # 방문했는지 확인
length = [] # 어떤 노드 ~ 다른 노드까지의 길이
for i in range(n) :
temp_input = list(map(int, input().split())) # 우선 한 줄 입력받기
j = 1
while temp_input[j] != -1 :
graph[temp_input[0]].append((temp_input[j], temp_input[j+1])) # -1이 입력되기 전까지 연결된 노드, 거리를 저장
j += 2
def DFS(node, temp) :
visited[node] = 1 # 일단 이 노드는 방문 처리
for child_node, distance in graph[node] :
if visited[child_node] == 0 : # 자식 노드에 방문 안 했다면
DFS(child_node, temp + distance)
length.append([temp, node]) # 방문 안 한 자식 노드가 없다면 -> 리프 노드라면 길이 저장
DFS(1, 0) # 시작 노드를 0부터 시작하도록 조정
temp_maxLength = max(length, key = lambda x: x[0])
diameter_point1 = temp_maxLength[1]
visited = [0] * (n+1)
length = [] # 배열들 초기화
DFS(diameter_point1, 0)
maxLength = max(length, key=lambda x: x[0])
print(maxLength[0]) # 최대 길이 출력시행착오
먼저, 처음에 코드를 짤때는 DFS의 매개변수에 노드 번호만 전달하고, 거리는 temp라는 변수에 더해가며 구하려고 했습니다. 그런데 그냥 매개변수에 거리도 전달하는 것이 더 깔끔하고 재귀 호출 과정에서의 예상치 못한 값 변경 등도 막을 수 있단 걸 알게 돼서 매개변수로 전달하는 방식으로 수정하였습니다.
또, 파이썬에서는 재귀함수 호출의 최댓값이 보통 1000회 정도로 돼있습니다. 근데 여기서는 1000회를 거뜬히 넘길 수 있어 sys 라이브러리를 import한 뒤 재귀함수 호출 최댓값을 늘렸어야 했는데 이를 인지하지 못하고 코드를 짜서 시간초과가 계속해서 났습니다. 따라서 sys.setrecursionlimit() 함수를 통해 재귀 호출 최댓값을 늘림으로써 에러를 해결할 수 있었습니다.
느낀 점
이 문제가 지금까지 풀었던 문제들 중 가장 저에게 도움이 된 문제 중 하나였던 것 같습니다. 정말 많이 쓰이지만 제가 어떻게 쓰는지를 몰라서 많은 문제들을 풀지 못하게 한 것들이 그래프, 트리, DFS, BFS 등이었는데 이번 문제를 푸는 과정을 통해 트리와 DFS에 대해 자세히 알게 되어 정말 좋은 경험이었던 것 같습니다. 특히 DFS를 직접 구현하는데 생각보다 어렵지 않은 알고리즘이라는 생각이 들었고, 앞으로도 DFS를 이용하는 문제를 풀 때 자신감을 가질 수 있을 것 같습니다.
'프로그래밍 > 문제 풀이' 카테고리의 다른 글
| 나만의 문제 만들기 - [AP 프로그래밍 - 7월 과제] (2) | 2024.07.01 |
|---|---|
| 백준(BaekJoon) 16434번 풀이 - [AP 프로그래밍 - 6월 과제] (0) | 2024.06.01 |
| 백준(BaekJoon) 1918번 풀이 - [AP 프로그래밍 - 4월 과제] (5) | 2024.04.01 |
| 백준(BaekJoon) 17951번 풀이 - [AP 프로그래밍 - 3월 과제] (3) | 2024.03.23 |



