2024.06.01 - [프로그래밍/강화학습 (RL)] - 틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 6월 과제]
틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 6월 과제]
2024.05.31 - [프로그래밍/강화학습 (RL)] - 틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 5월 과제] 틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 5월 과제]2024.04.08 - [프로그래밍/강화학
olzl07.tistory.com
드디어 3월부터 달려온 대장정이 끝나갑니다. 이번 달에는 3월부터 6월까지의 내용을 다 정리하고, 연구의 부족분을 채워보도록 하겠습니다.
문제 인식
저는 어렸을 때부터 게임을 만드는 활동에 흥미가 있었고, 관심을 가지고 있었습니다. 그래서 실제로 엔트리나 스크래치 등의 프로그래밍 언어를 이용해 게임을 만들어보기도 했는데, 고등학교에 들어와서 AI 학습 방법 중 하나인 강화학습이란 것을 알게 되었고, 게임 AI를 만드는 활동에 큰 흥미를 느끼게 되어 이번 정융탐의 주제로 고르게 되었습니다. 강화학습을 이용해 만들 수 있는 게임 AI의 종류는 무궁무진한데, 저는 이 중 세계적으로 유명하기도 하고 여러 게임들 중 상대적으로 게임의 룰이나 강화학습의 난이도가 낮은 틱택토를 선정하였습니다.
관련 조사 시행
강화학습에 대한 여러 자세한 이론들은 다음 글에서 다룰 예정이기에 이번에는 정말 간단한 요소들과 틱택토를 강화학습하는데에 필요한 여러 지식들에 대해서만 다뤄보겠습니다.
1. 용어 설명
(1) 강화학습 (Reinforcement Learning)
강화학습은 기계 학습의 한 영역으로, 어떤 환경 안에서 정의되어있는 에이전트(AI 등)가 현재의 상태를 인식해, 선택 가능한 행동들 중 보상을 최대화하는 행동을 선택하는 방법을 의미합니다. 강화학습은 복잡한 환경에서 최적의 해결책을 찾는 상황에 많이 이용되는데, 로봇, 자율주행 등에서 사용되며 특정 상황에서 최대 보상을 찾는 것이기 때문에 많은 게임들이 강화학습에 적합합니다. 바둑 AI 알파고 등이 강화학습을 이용한 가장 유명한 예입니다.
- 강화학습의 구성 요소
강화학습은 에이전트, 환경, 상태, 보상, 에피소드, 정책, 가치 함수 등의 요소로 구성됩니다.
| 에이전트(Agent) | 학습을 수행하는 대상 |
| 환경(Environment) | 에이전트가 상호작용하는 대상 |
| 상태(State) | 에이전트가 환경에 대해 파악할 수 있는 정보 |
| 보상(Reward) | 에이전트가 취한 액션에 대한 결과 (양수, 음수 다 가능) |
| 에피소드(Episode) | 에이전트가 최종 상태에 도달하며 보상을 얻는 과정 |
| 정책(Policy) | 에이전트가 상태를 입력받아 취해야 할 액션을 출력하는 함수 |
| 가치 함수(Value Fuction) | 특정 상태에서 받을 수 있는 보상을 예측하는 함수 |
(2) 틱택토 (Tic-Tac-Toe)
틱택토는 두 명이 번갈아가며 O와 X를 3x3 판에 써서 같은 글자를 가로, 세로 혹은 대각선상에 놓이게 하는 놀이입니다. 이 글을 읽을 모두가 알 정도로 정말 유명한 게임이며, 선 4개와 O, X만 있으면 되기에 아주 간단하게 즐길 수 있는 놀이입니다. 이런 유명성과 간단함 때문에 강화학습을 비롯한 여러 게임 관련 프로젝트 등에 자주 쓰이고 있고, 저도 이런 이유들로 인해 틱택토를 강화학습의 대상으로 선정하였습니다.
문제 해결 방안 설계
이 프로젝트는 보통 일반적으로 강화학습 프로젝트를 진행되듯이 진행할 것입니다. 강화학습은 보통 '환경 설정 - 문제 정의 - 에이전트 생성 - 학습 진행 - 훈련 및 검증'의 단계로 진행되기에, 이 단계에 맞춰 진행해보겠습니다.
1. 환경 설정
먼저, 에이전트와 환경 간 인터페이스 등 에이전트가 운영될 환경을 설정해야 합니다. 제 경우에는 틱택토 게임판, 틱택토의 기본적인 룰 등이 환경에 들어갑니다. 파이썬을 이용하여 환경을 설정하는 것이 가능하기 때문에 저는 파이썬으로 환경 설정을 할 것입니다.
2. 문제 정의
다음으로, 문제를 정의해야 합니다. 에이전트, 상태, 행동 등을 정의하고 특히 보상을 어떻게 줄지를 정해야 합니다.
3. 에이전트 생성
이후 에이전트를 생성해야 합니다. 에이전트를 생성할 때는 적절한 훈련 알고리즘을 선택해야 합니다. 알고리즘은 일반적으로 Q-Learning을 사용하기에 저도 Q-Learning을 이용해 학습을 시킬 예정입니다.
4. 훈련 및 검증
마지막으로 AI를 훈련시키고, 분석해야 합니다. 훈련을 진행하면 에이전트가 환경과 상호작용하며 정택에 따라 행동을 선택하고, 선택에 따른 보상을 받으며 이 보상을 최대화 할 수 있는 방안으로 정책이 개선되어 갑니다.이후, 에이전트의 여러 요소들을 분석해보며 학습이 잘 되었는지 확인해보았습니다.
이론적 배경
1. 마르코프 결정 과정 (Markov Decision Processes, MDP)
MDP(마르코프 결정 과정)는 강화학습의 큰 개념입니다. 강화학습이 이 큰 개념에서 잘 그려지고 요소들이 잘 정의되어야 좋은 결정을 한다고 할 수 있습니다. MDP의 구성 요소는 다음과 같습니다.

1) 상태 (S)
상태는 에이전트가 관찰 가능한 상태의 집합입니다. 어떤 시점 t에서 가지고 있는 상태 St들의 집합이 S인 것입니다.
2) 행동 (A)
행동은 어떤 상태 St에서 취할수 있는 행동을 의미합니다.
3) 상태 변환 확률 (P)
상태 변환 확률이란 내가 지금 하려는 행동에 의해 상태가 그대로 변하지 않고, 어떤 변수에 의해 의도한 상태와 다른 상태로 바뀌는 것입니다.
Pass′=P[St+1=s|St=s,At=a]
4) 보상 함수 (R)
보상함수는 에이전트가 학습할 수 있는 유일한 정보로, 환경이 에이전트에게 주는 정보입니다.
상태가 변하는 것 자체가 확률적이기에 보상을 얼마나 받느냐도 당연히 기댓값 ,즉 확률로써 나타납니다.
r(s,a)=E[Rt+1=s|St=s,At=a]
5) 감가율 (γ)
감가율은 0과 1 사이의 수로, 같은 크기의 보상이더라도 나중에 어느 정도의 가치가 되는지를 나타내는 것입니다.
결론적으로 마르코프 결정 과정은 위에서 봤듯이 상태에서 상태를 넘어다니며 확률적으로 변하는 것들을 모델링해주게 됩니다.
2. 벨만 방정식 (Bellman Equation)
벨만 방정식은 현재 상태의 가치 함수와 다음 상태의 가치 함수 사이의 관계를 식으로 나타낸 것입니다. 벨만 방정식을 알기 위해선 먼저 알아야 할 몇 가지 지식들이 있습니다.
1) 정책 (Policy)
정책이란 에이전트가 어떤 상황에서 취할 행동을 의미합니다.
그러나, 상태 변환 확률에서 말했듯 St에서 At는 확률적으로 이루어지기 때문에 이에 따른 정책 또한 확률로써 나타납니다. 정책은 조건부 확률로 나타나는데, "어떤 상태 s에서 행동 a를 취하는 것이 확률 p이다."라고 표현됩니다.
π(a|s)=P[At=a|St=s]
이를 이용해 시점 t부터 현재 시점 k까지 받은 보상 Gt를 구할 수 있습니다.
Gt=Rt+1+r1Rt+2+r2Rt+3...+rk−1Rt+k
2) 가치 함수 (Value Function)
가치 함수는 내가 받을 수 있는 보상을 함수로 표현한 것입니다. 당연히 얘도 확률적으로 표현되고요. 가치 함수는 어떤 상태 s에서 받는 보상을 예측하는 상태 가치 함수와 어떤 상태 s에서 어떤 행동 a를 취했을 때 받는 보상을 예측하는 행동 가치 함수로 나뉘게 됩니다.
i) 상태 가치 함수 (State Value Function)
vπ(s)=Eπ[Gt|St=s]
=Eπ[Rt+1+γRt+2+γ2Rt+3+...|St=s]
=Eπ[∑k=0γkRt+k+1|St=s]
ii) 행동 가치 함수 (Action Value Function)
qπ(s,a)=Eπ[Gt|St=s,At=a]
=Eπ[Rt+1+γRt+2+γ2Rt+3+...|St=s,A−t=a]
=Eπ[∑k=0γkRt+k+1|St=s,At=a]
3) 벨만 방정식 (Bellman Equation)
벨만 방정식은 현재 상태와 다음 상태의 가치 함수 사이의 관계를 나타낸 것으로 다음과 같은 식으로 나타납니다.
vπ(s)=Eπ[Rt+1+γvπ(St+1)+|St=s]
3. 시간차 학습 (Temporal Differance Learning, TD)
TD(시간차 학습)는 에피소드 전체를 보지 않고 바로바로 업데이트가 진행됩니다. TD의 가치 함수 업데이트는 다음과 같습니다.
V(St)←V(St)+α(Rt+1+γV(St+1)−V(s))
이때, Rt+1+γV(St+1)은 Gt로 나타낼 수 있습니다.
1) SARSA 방식
SARSA는 TD의 한 종류입니다. 이름이 SARSA인 이유는 St,At,Rt+1,St+1,At+1을 사용하기 때문입니다. St+1에서의 정책에 따른 At+1까지 고려해준다고 이해하시면 될 것 같습니다. SARSA의 Q-함수 업데이트는 다음과 같습니다.
Q(St,At)←Q(St,At)+α(Rt+1+γQ(St+1,At+1)−Q(St,At))
2) Q-Learning
Q-Learning은 현재 강화학습에서 가장 자주 쓰이는 방법이고, Q_Learning에서의 Q-함수 업데이트는 다음과 같습니다.
Q(St,At)←Q(St,At)+α(Rt+1+γQ(St+1,a′)−Q(St,At))
SARSA와의 차이점은 At가 a'로 바뀌었다는 것밖에 없습니다. 이때 a'은 St+1에서 가장 높은 행동 가치 함수 값을 가지는 행동을 의미합니다.
즉, SARSA는 정책에 따른 다른 행동을 고려하고 Q-Learning에서는 정책을 신경쓰지 않고 최적의 다음 행동(이라고 학습된 것)만 고려하는 것입니다.
순서도
환경을 구축하기에 앞서, 어떤 방식으로 코드를 짤지를 순서도를 통해 알아보겠습니다.
먼저, 기본적인 틱택토 플레이 코드의 순서도는 다음과 같습니다.
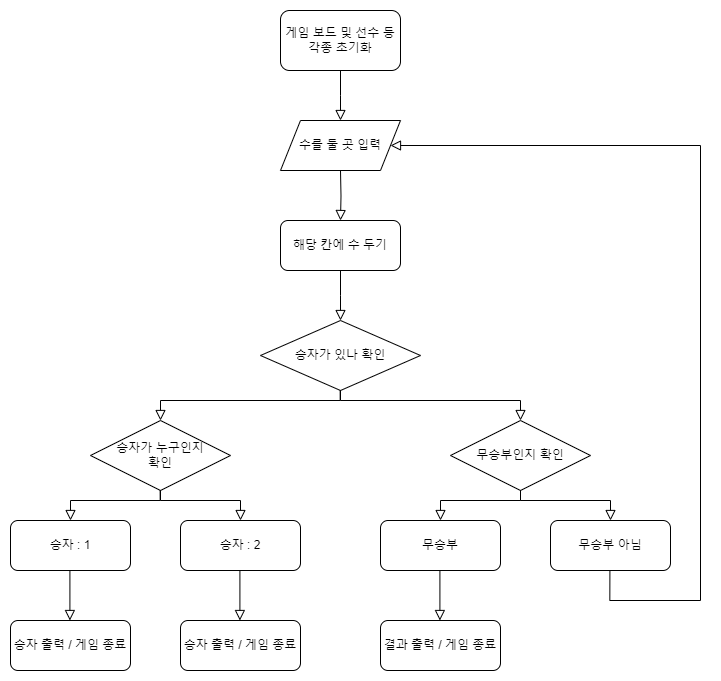
이 코드를 구현하기 위해서는 초기화 메서드, 보드 출력 메서드, 착수 메서드, 승자 확인 메서드, 빈 칸 확인 메서드 등 여러 메서드가 필요합니다.
환경 구현
이제 앞서 짠 순서도와 의사코드들을 바탕으로 2명의 플레이어가 틱택토를 플레이 할 수 있는 환경을 구축해보겠습니다.
먼저, 클래스를 설정하고 초기화 메서드를 지정해줄 것입니다. 초기화 메서드는 앞서 말했듯이 init 생성자로 만들어 객체가 생성되자마자 실행되게 할 것입니다.
보드를 모두 0으로 초기화해주고, 승리할 수 있는 조건들을 지정해준 뒤 승자를 0, 플레이어를 -1로 초기화해줄 것입니다. (플레이어를 -1로 초기화하는 이유는 보통 틱택토는 X가 먼저 두기 때문입니다)
저는 앞으로 1을 O, -1을 X로 생각하고 프로그래밍을 할 것입니다.
이후 보드를 print하는 코드를 짜주었습니다. 반복문을 이용해 board 내의 모든 요소들을 돌며 요소가 0이면 빈칸, 1이면 O, -1이면 X를 저장하도록 하였고, 가독성을 위해 열과 열 사이를 ' | '로 구분하여 출력되게 하였습니다. ' | '로 구분하는 것을 위해 join 함수를 사용하였습니다.
다음으론 착수 메서드를 짜보았습니다. 착수할 위치 num을 매개변수로 입력받고, 어차피 학습시킬때 이러한 오류가 날 일은 없겠지만 혹시 모르므로 우선 num이 0 미만 8 초과이거나 num 위치가 이미 차있으면 False를 반환하게 하였습니다.
이후 O와 X를 구분하는 1, -1과 플레이어의 정보 1, -1이 서로 같으므로 착수할 위치의 요소에 현재 플레이어의 값을 저장해주면 됩니다. 이후 플레이어를 변경하였습니다.
착수를 마친 후에는 승자가 있는지 판단하여 승자가 있으면 승자를 출력하고 게임을 종료시켰습니다. 승자가 없다면 모든 칸이 다 찼는지를 확인해 무승부인지를 판단하여 무승부라면 무승부라고 출력하고 게임을 종료하게 했고, 무승부도 아니라면 그냥 게임이 이어지게 하였습니다. 게임이 종료될때는 True,이어질때는 False를 반환하게 하여 게임 종료를 판단하게 만들었습니다.
승자가 있는지를 판단하는 코드도 짜보았습니다. 앞서 지정한 승리 조건들의 모든 조건에 대해 보드의 요소들 중 1 혹은 -1이 전부 그 조건에 들어간다면 승자를 해당 플레이어로 지정하고, 함수를 종료하였습니다. 만약 여기서 승자를 가리지 못한다면 보드가 비어있는지를 확인해서 비어있지 않다면 승자를 None으로 지정해 무승부라고 표기하고 함수를 종료하였습니다. (이 코드 짜면서 all 함수를 처음 써봤는데 이런 함수도 다 쓸데가 있구나~라는 걸 깨닫게 되었습니다.)
마지막으로 보드에 빈 칸이 있는지를 확인하는 메서드를 짜겠습니다. 간단하게 리스트 내에 0이 있는지를 판단하여 True 혹은 False를 반환하게 하는 방식으로 구현할 수 있었습니다.
코드 수정 및 개발 마무리
이후 입력을 키패드로 받게 바꾸고, 기보 시스템을 추가하고, 승리 조건을 확인하는 방법을 변경하고, 플레이어 간의 구분 기능과 보상 설정, 전이확률 제작 등 강화학습에 필요한 여러 코드들을 넣어 환경을 수정하였습니다.
또, 학습률, 감가율, 입실론 등을 이용해 Agent를 정의하는 생성자와, q_value가 최대인 행동을 선택하는 함수, q_value를 조정해가는 함수 등이 포함되어있는 Agent에 관한 Agent 파일과, episode 수만큼 반복하여 경기를 하며 q_learning을 진행하는 코드와 그 과정에서의 최종 보상, 승률 등을 그래프로 출력해주는 함수, 승률을 계산하는 코드 등으로 구성된 Q-learning을 작동시키는 코드인 run_q_learning 파일을 제작하였습니다.
코드들은 다음과 같습니다.
1. 환경 코드
import random
from collections import defaultdict
class TicTacToe() :
def __init__(self, player_mode = '1p', print_mode = "Y") :
if player_mode == '1p':
self.mode = 1
elif player_mode == '2p':
self.mode = 2
else :
print("error - default mode : 1p")
self.mode = 1
if print_mode != "N" and print_mode != "Y":
self.print_mode = "N" #wrong input : defalut setting
else:
self.print_mode = print_mode
self.cell = 3
self.answer = [] # 승리 조건들
for i in range(self.cell) :
self.answer.append([i*self.cell + j for j in range(self.cell)])
self.answer.append([j*self.cell + i for j in range(self.cell)])
self.answer.append([i*self.cell + i for i in range(self.cell)])
self.answer.append([i*self.cell + self.cell-(i+1) for i in range(self.cell)])
self.reward_case = {"win" : 6.0,
"lose" : -2.0,
"draw" : -1.0,
"wrong_move" : -5.0,
"nothing" : 0.0}
n_state = 3**(self.cell**2)
n_action = self.cell**2
P = defaultdict(dict)
for s in range(n_state):
before_board = self.state2board(s)
temp_board = self.state2board(s)
P[s] = defaultdict(list)
for a in range(n_action):
temp_board[a] = 1
next_s = self.board2state(temp_board)
done, winner = self.check_win(temp_board)
if done:
if winner == 1:
r = self.reward_case["win"]
elif winner == -1:
r = self.reward_case["lose"]
elif winner == 0:
r = self.reward_case["draw"]
else:
r = self.reward_case["nothing"]
if before_board[a] != 0:
r = self.reward_case["wrong_move"]
else:
r = self.reward_case["nothing"]
if self.check_win(before_board)[0]:
game_over = True
next_s = s
else:
game_over = False
P[s][a] = [(1.0, next_s, r, game_over)]
self.reset()
self.print_board()
def reset(self) :
self.board = [0] * (self.cell)**2
self.winner = 0
self.player = 1
self.notation = []
def print_board(self) :
if self.print_mode == "N":
return
for i in range(self.cell) :
row = []
print('-------------')
for j in range(self.cell) :
item = self.board[self.cell*i + j]
if item == 0 :
row.append(' ')
elif item == 1 :
row.append('O')
else :
row.append('X')
print(f'| {" | ".join(row)} |')
print('-------------\n')
def move(self, action) :
before_empty = True
if self.board[action] != 0:
before_empty = False
self.board[action] = self.player
self.player *= -1
self.notation.append(self.board.copy())
done, self.winner = self.check_win(self.board)
reward = self.reward_case["nothing"]
if done :
if self.winner == 1 :
print("Player 1 Win!!")
reward = self.reward_case["win"]
elif self.winner == -1 :
print("Player 2 Win!!")
reward = self.reward_case["lose"]
else :
print("Draw!!")
reward = self.reward_case["draw"]
if not before_empty:
reward = self.reward_case["wrong_move"]
return (self.board2state(self.board), reward, done)
def check_win(self, board) :
for condition in self.answer :
if all(board[i] == 1 for i in condition) :
return (True, 1)
elif all(board[i] == -1 for i in condition) :
return (True, -1)
if not self.empty(board) :
return (True, 0)
else:
return (False, 0)
def empty(self, board) :
if 0 in board :
return True
else :
return False
def get_input(self) :
if self.mode == 1 and self.player == -1:
while(True):
n = random.randint(0, self.cell**2 - 1)
if self.board[n] == 0:
self.move(n)
break
else:
n = input()
if n.isdigit() :
n = int(n) - 1
if 0 <= n <= self.cell**2 - 1 :
if self.board[n] == 0 :
self.move(n)
else :
print("비어있는 칸에 착수하세요\n")
else :
print(f"착수할 수 있는 칸은 1에서 {self.cell**2} 사이입니다\n")
else :
print("정수로 입력하세요\n")
def board2state(self, board):
res = 0
for i in range(9):
res += board[i]*(3**i)
return res
def state2board(self, state):
res = [0]*9
for i in range(9):
res[i] = state%3
state == (int)(state/3)
return res
2. Agent 코드
from collections import defaultdict
import numpy as np
class Agent() :
def __init__(self, env, alpha = 0.1, gamma = 0.9, epsilon = 0.9, epsilon_min = 0.1, epsilon_dacay = 0.95) :
self.env = env
self.alpha = alpha
self.gamma = gamma
self.epsilon = epsilon
self.epsilon_min = epsilon_min
self.epsilon_decay = epsilon_dacay
self.q_table = defaultdict(lambda : np.zeros(self.env.cell ** 2))
def choose_action(self, state):
available_actions = [i for i, v in enumerate(self.env.board) if v == 0]
if np.random.uniform() < self.epsilon:
action = np.random.choice(available_actions)
else:
if state not in self.q_table:
self.q_table[state] = np.zeros(self.env.cell ** 2)
q_values = self.q_table[state]
perm_actions = np.random.permutation(available_actions)
action = perm_actions[np.argmax([q_values[a] for a in perm_actions])]
return action
def learn(self, transition) :
s, a, r, next_s, done = transition
q_value = self.q_table[s][a]
if done :
q_target = r
else :
q_target = r + self.gamma * np.max(self.q_table[next_s])
self.q_table[s][a] += self.alpha * (q_target - q_value)
if self.epsilon > self.epsilon_min :
self.epsilon *= self.epsilon_decay
3. Q-learning 코드
from TTT_Env import TicTacToe
from agent import Agent
from collections import namedtuple
import matplotlib.pyplot as plt
import numpy as np
np.random.seed(1)
Transition = namedtuple('Transition', ('state', 'action', 'reward', 'next_state', 'done'))
def Run_Q_Learning(agent, env, num_episode, p_mode = "N"):
history = []
for episode in range(num_episode):
state = env.reset()
final_reward, n_moves = 0.0, 0
while True:
action = agent.choose_action(state)
next_state, reward, done = env.move(action)
agent.learn(Transition(state, action, reward, next_state, done))
env.print_board()
state = next_state
n_moves += 1
if done:
final_reward = reward
break
history.append(final_reward)
if episode%1 == 0:
print('에피소드 %d: 보상 %.1f #이동 %d' %(episode, final_reward, n_moves))
return history
def plot_learning_history(history, env):
win_prob = win_prob_history(history, env)
fig = plt.figure(1, figsize=(14, 10))
ax = fig.add_subplot(2, 1, 1)
plt.plot(history, 'b.')
plt.xlabel('Episodes')
plt.ylabel('Final Rewards')
ax = fig.add_subplot(2, 1, 2)
plt.plot(win_prob)
plt.xlabel('Episodes')
plt.ylabel('Winning Probability')
plt.show()
def win_prob_history(history, env):
win_r = env.reward_case["win"]
res = []
win_n = 0
for i in range(len(history)):
if history[i] == win_r:
win_n += 1
res.append(win_n/(i+1))
return res
env = TicTacToe("1p", "N")
agent = Agent(env)
history = Run_Q_Learning(agent, env, 10000)
plot_learning_history(history, env)실행 결과 및 분석
코드를 실행한 결과 출력된 그래프들은 다음과 같습니다.
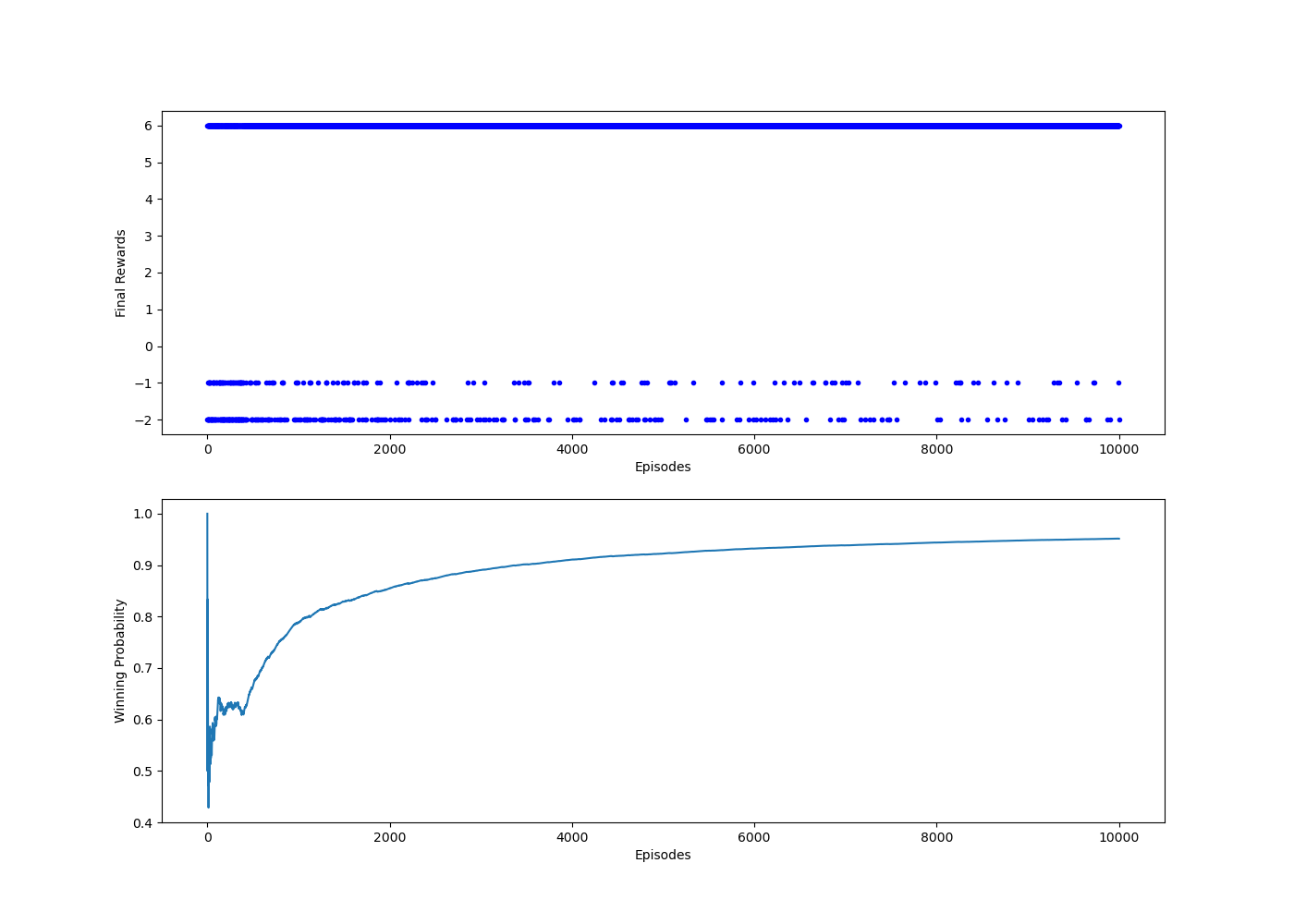
그래프를 잠깐 살펴보면 최종 보상이 6(승리), -1(무승부), -2(패배)로 구성되어있는데 그 중 에이전트 1이 승리한 경우 (6)가 압도적으로 많은 걸 살펴볼 수 있고, 승률도 계속해서 올라가는 것으로 보아 에이전트 1의 강화학습이 아주 잘 진행되었다고 볼 수 있을 것 같습니다.
소감
처음 과제를 시작할때는 참 막막했던 것 같은데 시작하고 차례차례 과제를 수행해나가니 재미있었던 것 같습니다. 이해하기가 조금 어렵긴 했지만 주제와 관련된 이론적 배경들을 탐구하거나 순서도를 만드는 과정이 특히 재미있었던 것 같습니다.
가장 기억에 남았던 것은 환경을 설정하는 코드를 짜는 건데 틱택토의 규칙에 맞게 클래스와 각종 메서드들을 제작해나가는 것이 실제로 게임을 만드는 것 같은 기분이 들었습니다. 또 어렸을 때부터 엔트리 등에서 게임을 만들어봐서 그런지 이 과정이 많이 재미있었던 것 같고, 블록을 이용해 코드를 짜는 엔트리보다 좀 더 밑바닥부터 전문적으로 만들어가서 그런지 더 자랑스러웠던 것 같습니다.
마지막에 최종적으로 강화학습을 시키고 분석을 해봤을 때 학습시킨 Agent가 훨씬 많이 이기고, 승률이 높은 걸 보며 학습이 잘 됐다고 느껴 기분이 좋았습니다. 중간중간 힘든 일도 많고 고생도 많이 해서 그런지 완성시켰을 때 오는 성취감이 훨씬 컸던 것 같습니다. 아쉬운 점은 Agent가 어떤 칸에 처음 놨을 때 승률이 어떤지 등 좀 더 다양한 요인들을 분석해보고 싶었는데 조졸시험 준비해야해서 시간이 좀 부족해서 하지 못한 게 아쉽습니다. 나중에 방학하고 나서 꼭 분석을 해보도록 해야겠습니다.
'프로그래밍 > 틱택토 강화학습 (TTT-RL)' 카테고리의 다른 글
| 틱택토 강화학습 (Tik-Tak-Toe RL) - [심화 탐구] (2) | 2024.08.12 |
|---|---|
| 틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 6월 과제] (0) | 2024.06.29 |
| 틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 5월 과제] (4) | 2024.05.31 |
| 틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 4월 과제] (2) | 2024.04.13 |
| 틱택토 강화학습 (Tik-Tak-Toe RL) - [정보과학융합탐구 - 3월 과제] (1) | 2024.03.28 |



